In order to emphasize the diversity order created by coding at the transmitter side,
all computer simulations have been conducted with the number of receive antennas 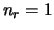 .
Figures 4 and 5 illustrate the word error rate performance
of a space-time BICM for
.
Figures 4 and 5 illustrate the word error rate performance
of a space-time BICM for 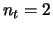 transmit antennas,
transmit antennas, 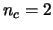 channel states,
channel states, 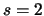 time period
spreading and a coding rate
time period
spreading and a coding rate 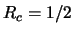 . Figure 4 illustrates the case with
. Figure 4 illustrates the case with
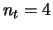 transmit antennas and a precoding spread factor
transmit antennas and a precoding spread factor 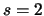 .
At the first iteration, for
.
At the first iteration, for 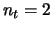 , IOM precoding slightly outperforms other rotations.
After 10 detection/decoding iterations, IOM is outperformed by G-IOM and other algebraic rotations.
The slight difference in performance is still apparent for
, IOM precoding slightly outperforms other rotations.
After 10 detection/decoding iterations, IOM is outperformed by G-IOM and other algebraic rotations.
The slight difference in performance is still apparent for 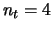 .
.
Figure 4:
Word error rate of ST-BICM at iterations 1 and 10. MIMO channel
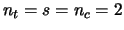 ,
, 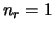 . Interleaver size
. Interleaver size 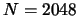 bits,
rate 1/2 16-state
bits,
rate 1/2 16-state  convolutional code. QPSK modulation.
convolutional code. QPSK modulation.
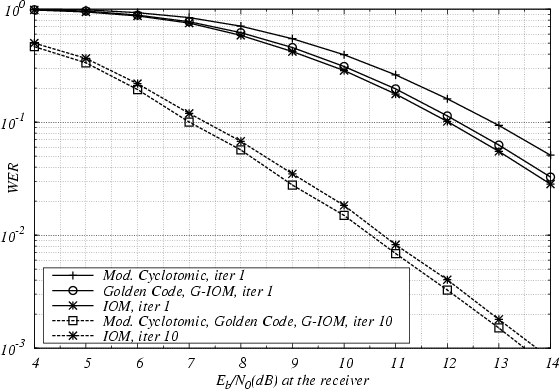 |
Figure 5:
Word error rate of ST-BICM versus outage limit. MIMO channel
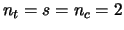 ,
, 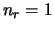 . Interleaver size
. Interleaver size 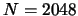 bits,
rate 1/2 16-state
bits,
rate 1/2 16-state 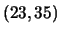 convolutional code. QPSK modulation.
convolutional code. QPSK modulation.
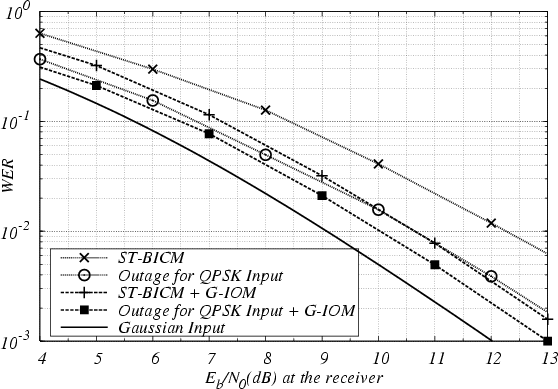 |
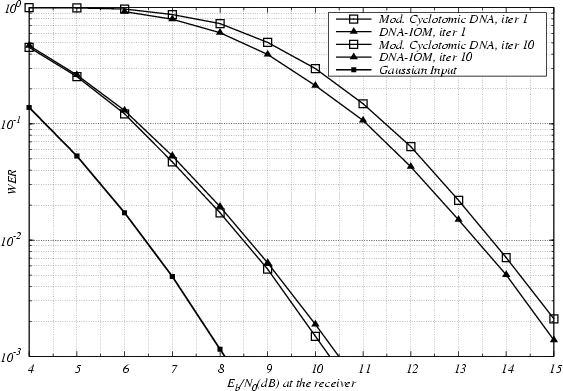
Figure 6:
Word error rate of ST-BICM at iterations 1 and 10 versus outage limit with gaussian input. MIMO channel 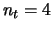 ,
, 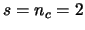 ,
, 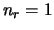 . Interleaver size
. Interleaver size 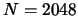 bits, rate 1/2 16-state
bits, rate 1/2 16-state 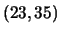 convolutional code. QPSK modulation.
convolutional code. QPSK modulation.
 |
From the observed performance and the flexibility of linear precoders, we conclude the following.
Cyclotomic rotations satisfying genie/DNA conditions are the best choice for precoding
in space-time bit-interleaved coded modulations. These rotations are optimal in both algebraic
and information theoretical senses. They exist for any set of MIMO channel parameters,
mainly the number of transmit antennas and the precoder time-spreading factor.
Joseph Jean Boutros
2005-05-07

