Consider a multiple-input multiple-output system with 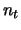 transmit and
transmit and 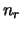 receive antennas.
The channel is supposed to be frequency non-selective (no inter-symbol interference) and known to the receiver but not to the transmitter (CSI at the receiver side only). The number of independent channel realizations observed during one codeword transmission is denoted by
receive antennas.
The channel is supposed to be frequency non-selective (no inter-symbol interference) and known to the receiver but not to the transmitter (CSI at the receiver side only). The number of independent channel realizations observed during one codeword transmission is denoted by 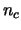 . The parameter
. The parameter 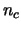 takes values from 1 (quasi-static fading) up to the codeword time length (ergodic channel). The input-output channel model is given by
takes values from 1 (quasi-static fading) up to the codeword time length (ergodic channel). The input-output channel model is given by
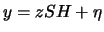 |
(1) |
where
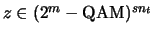 ,
, 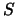 is the linear precoder matrix (also called full-rate space-time block code in the MIMO community) of size
is the linear precoder matrix (also called full-rate space-time block code in the MIMO community) of size
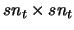 . The integer parameter
. The integer parameter 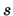 represents the time spreading of the precoder,
represents the time spreading of the precoder,
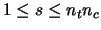 . We restrict our study to unitary precoders, i.e.,
. We restrict our study to unitary precoders, i.e.,
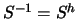 . The
. The
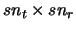 MIMO channel matrix
MIMO channel matrix 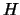 has
has 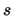 blocks on its diagonal and zeros elsewhere. Each block is associated to the transmission over the
blocks on its diagonal and zeros elsewhere. Each block is associated to the transmission over the
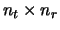 MIMO channel during one channel use. We can see
MIMO channel during one channel use. We can see 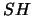 as a new correlated MIMO channel and call a precoding time period the group of
as a new correlated MIMO channel and call a precoding time period the group of 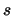 channel uses associated to the matrix
channel uses associated to the matrix 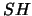 . Finally,
. Finally,
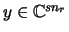 is the channel output and
is the channel output and 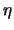 is an additive white gaussian noise with zero mean and variance
is an additive white gaussian noise with zero mean and variance 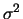 per real component.
per real component.
Joseph Jean Boutros
2005-05-07